I have taken a step back and learned a little bit about what Linear Regression actually is. As far as I can tell, it’s what I have described here with the red and blue dots. It’s not a “neural network” at all in the sense that it has no hidden layers. That’s how I think of a neural network anyway, it doesn’t really get interesting until you have hidden layers. That might not be the official definition though.
I am also refreshing my memory on what the hidden layers actually do. It seems they combine the functions from previous layers in order to approximate functions that are non-linear. So my red-and-blue-dots picture for networks with a hidden layer would look more like this:
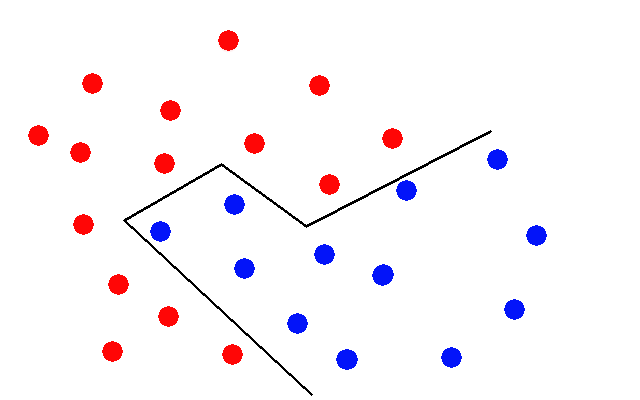
And as you add more layers you combine these more complicated functions, and of course it’s all in hundreds of dimensions so it can get quite complicated.
It also makes sense that the more layers you have, the more danger there is of “overfitting”. It is hard to over-fit with a straight line, but with an arbitrarily complicated series of segments you could carve out a little spot for each data point and ignore everything else.
Taking this back to my lousy keras model, we can approximate scikit’s LinearRegression() model with something more like this:
# build model
elmo_input = Input(shape=(1024,), dtype="float")
pred = Dense(1, activation='linear')(elmo_input)
model = Model(inputs=[elmo_input], outputs=pred)
model.compile(loss='mse', optimizer='sgd', metrics=['accuracy'])I got ideas for the various parameters from this fella. Anyway this model behaves much more like the scikit one; it’s not perfect, but it gives different answers for different inputs and the answers seem pretty good from an intuitive standpoint.
So what can we learn from this? It seems that the magic stuff going on in ELMo makes their output vectors pretty well suited to linear regression. That’s pretty handy, since linear regression is easy! Doing something fancier is going to take a little more work in adjusting parameters, because there are more things to adjust.
